インターネットで特殊相対性理論の話を見たのですが、おかしな話だと思うんですけどね。(^^;
今回も、私の視点から考えてみたいと思います。
今回は、次の話の続きです。
1.一体時間とは何なのか?時間は止まるのか?
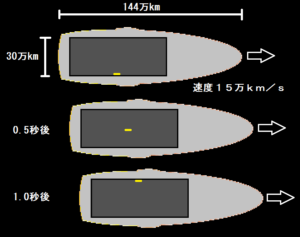
大きすぎるロケットですが、ロケットに付いている窓の高さが30万Km、ロケットの奥行きが144万Km、ロケットの速度が15万Km/秒、光の速度は30万Km/秒とします。
インターネットから伝わる話によると、ロケットから光を発したとき、次のように光が動くらしいのです。
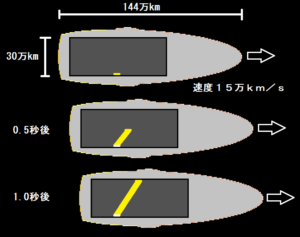
元々光があった位置を白で表すと、光は図の様に動いたことに成ります。
これは、ロケットの移動速度に光が影響されていることを示し、光は上へ30万Km/秒、横へ15万Km/秒で移動しているということになります。
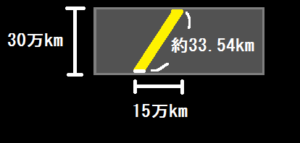
光の移動速度は30万Km/秒なので、次のように光が天井へ到達する時間が掛かることになります。
33.54万Km÷30万Km=1.118秒

実は、ロケットの中で起きていることは、地球では少し送れて見えます。
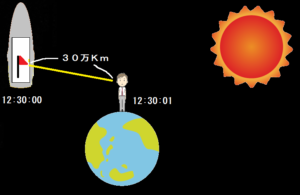
例えば、ロケットと地球で時計の時間を合わせたとします。
ロケットで12:00分00秒に赤い旗を上げたとします。
ロケットと地球上の人までの距離が30万Kmだったとすると、赤い旗の光が地球にいる人へ届くまで1秒掛かります。
つまり、地球上では12:00分01秒後に赤い旗が建つという事が分かります。
通常、色は物体が吸収せずに反射した色が人の目へ入射することにより色を識別します。
つまり旗へ光が当たり、旗が反射する赤色の光が人の目へ入ることにより、赤い旗だと認識するということです。
この赤い光も同じ光なので、30万Km先の人へ赤い光が届くまでの時間は1秒。
つまり、ロケットの中で赤い旗を建て、1秒後に地球上の人は赤い旗が建ったと気づきます。
特殊相対性理論では時間が遅れるという話ですが、私はそう思いません。(^^;
インターネットの話でも学問であっても、どこまでが事実なのか分からないのですが、間違いが含まれているかもしれませんので、一意見として注意しながら情報を捉えてください。
以上。
