月: 2021年9月

今回は、正則行列の逆行列を複雑な実例を元に算出したいと思います。

４×４行列も３×３行列でも計算方法は変わらないので、簡単な３×３行列を使って説明しようと思います。

今回は、次の話の続きです。
１．３次元計算では左手系座標系の方が理解し易い
２．３次元空間の回転方向とおかしな例
私は左手系座標系を使い、時計回りに回転させています。

今回は、コンピューターで計算した結果から小数点を切り捨てて使用していますので、四則演算の計算結果に多少誤差があります。
例
1.0÷3.0=0.33333333333333333333333333333333
0.33333333333333333333333333333333×3.0
=0.99999999999999999999999999999999

1-0.99999999999999999999999999999999
=0.00000000000000000000000000000001（誤差）
誤差の計算。

小数点を切り捨てると
0.3333

0.3333×3.0=0.9999
1.0-0.9999=0.0001（誤差）
切捨てを頻繁にしていることと、計算結果と整合性を保つ意図から、1.0÷3.0=0.33, 1.0-0.33=0.66の様にずれます。

誤差の例
2.4184-2.4184, 7.0710-(-7.0709), 6.6446-6.6443, 0.0-(-1.0), 1.0-0.0, 0.0-0.0
本当の答え
=0.0, 14.1419, 0.0003, 1.0, 1.0, 0.0
つじつまを合わせる答え
=0.0, 14.1421, 0.0, 1.0, 1.0, 0.0

まずは、計算元となるマトリックスを算出しましょう。

Ｚ軸を４５度回転させるマトリックス。

Ｙ軸を１１０度回転させるマトリックス。

各座標を１０倍へ拡大するマトリックス。

３つのマトリックスを掛け合わせた変換元の行列です。

次は、正則行列の逆行列を算出したいと思います。

掛け合わせたマトリックスから、逆行列を算出したいと思います。
まず、１行目の１列目を１にするには、-2.4184で変換元の行列、そして逆行列の１行目を割ります。
-2.4184÷(-2.4184)=1.0
-2.4184÷(-2.4184)=1.0
-9.3969÷(-2.4184)=3.885585511081706913661925239828
1.0÷(-2.4184)=-0.41349652662917631491895468078068
0.0÷(-2.4184)=0.0
0.0÷(-2.4184)=0.0

すると、図の様なマトリックスになります。
次は、２行目と３行目の１列目をゼロにします。

２行目１列目の-7.0710を１行目に掛け合わせます。
1.0000×(-7.0710), 1.0000×(-7.0710), 3.8855×(-7.0710), -0.4134×(-7.0710), 0.0000×(-7.0710), 0.0000×(-7.0710)
=-7.0710, -7.0710, -27.4743705, 2.9231514, 0.0, 0.0

求めた数で、２行目を引きます。
-7.0710-(-7.0710), 7.0710-(-7.0710), 0.0000-(-27.4743705), 0.0000-2.9231514, 1.0000-0.0, 0.0000-0.0
=0.0, 14.142, 27.4743705, -2.9231514, 1.0, 0.0

３行目１列目の6.6446を１行目に掛け合わせます。
1.0000×6.6446, 1.0000×6.6446, 3.8855×6.6446, -0.4134×6.6446, 0.0000×6.6446, 0.0000×6.6446
=6.6446, 6.6446, 25.8175933, -2.74687764, 0.0, 0,0

求めた数で、２行目を引きます。
6.6446-6.6446, 6.6446-6.6446,-3.4202-25.8175933, 0.0000-(-2.74687764), 0.0000-0.0, 1.0000-0.0
=0.0, 0.0, -29.2377933, 2.74687764, 0.0, 1.0

すると、図の様なマトリックスになります。

次は、２行目の２列目を１にしなければならないので、14.142136で変換元の行列、そして逆行列の２行目を割ります。
次は、２行目の２列目を１にしなければならないので、14.142136で変換元の行列、そして逆行列の２行目を割ります。
0.000000÷14.142136=0.0
14.142136÷14.142136=1.0
27.474764÷14.142136=1.9427591419004880168031194156243
-2.9238÷14.142136=-0.20674387518264567672097058039889
1.0÷14.142136=0.07071067623730955493569005417569
0.0÷14.142136=0.0

すると、図の様なマトリックスになります。

次は、３行目と１行目の２列目をゼロにします。

３行目２列目の0.0を２行目に掛け合わせます。
0.0000×0.0, 1.0000×0.0, 1.9427×0.0, -0.2067×0.0, 0.0707×0.0, 0.0000×0.0
=0.0, 0.0, 0.0, 0.0, 0.0, 0.0

求めた数で、３行目を引きます。
0.0000-0.0, 0.0000-0.0,-29.2380-0.0, 2.7474-0.0, 0.0000-0.0, 1.0000-0.0
=0.0, 0.0, -29.2380, 2.7474, 0.0, 1.0

１行目２列目の1.0を２行目に掛け合わせます。
0.0000×1.0, 1.0000×1.0, 1.9427×1.0, -0.2067×1.0, 0.0707×1.0, 0.0000×1.0
=0.0, 1.0, 1.9427, -0.2067, 0.0707, 0.0,

求めた数で、１行目を引きます。
1.0000-0.0, 1.0000-1.0, 3.8855-1.9427, -0.4134-(-0.2067), 0.0000-0.0707, 0.0000-0.0
=1.0, 0.0, 1.9427, -0.2067, -0.0707, 0.0

すると、図の様なマトリックスになります。

次は、３行目の３列目を１にしなければならないので、-29.2380で変換元の行列、そして逆行列の３行目を割ります。

0.0000÷(-29.2380)=0.0
0.0000÷(-29.2380)=0.0
-29.2380÷(-29.2380)=1.0
2.7474÷÷(-29.2380)=-0.09396675559203775908064847116766
0.0000÷(-29.2380)=0.0
1.0000÷(-29.2380)=-0.03420206580477460838634653533073

すると、図の様なマトリックスになります。

次は、１行目と２行目の３列目をゼロにします。

１行目３列目の1.9427を３行目に掛け合わせます。
0.0000×1.9427, 0.0000×1.9427, 1.0000×1.9427, -0.0939×1.9427, 0.0000×1.9427,-0.0342×1.9427
=0.0, 0.0, 1.9427, -0.18241953, 0.0, -0.06644034

求めた数で、１行目を引きます。
1.0000-0.0, 0.0000-0.0, 1.9427-1.9427, -0.2067-(-0.18241953),-0.0707-0.0, 0.0000-(-0.06644034)
=1.0, 0.0, 0.0, -0.02428047, -0.0707, 0.06644034

２行目３列目の1.9427を３行目に掛け合わせます。
0.0000×1.9427, 0.0000×1.9427, 1.0000×1.9427, -0.0939×1.9427, 0.0000×1.9427,-0.0342×1.9427
=0.0, 0.0, 1.9427, -0.18241953, 0.0, -0.06644034

求めた数で、２行目を引きます。
0.0000-0.0, 1.0000-0.0, 1.9427-1.9427, -0.2067-(-0.18241953), 0.0707-0.0, 0.0000-(-0.06644034)
=0.0, 1.0, 0.0, -0.02428047, 0.0707, 0.06644034

すると、図の様な逆行列が出来ます。

最後に、逆行列により元の数値へ戻るか確認したいと思います。

まず、マトリックスを使用しない場合にどうなるか考えてみましょう。

ベクトル(10.0, 20.0, 30.0)を変形させましょう。

左手系座標系でＺ軸を時計回りに４５度回転させると、(21.21, 7.07, 30.00)になります。

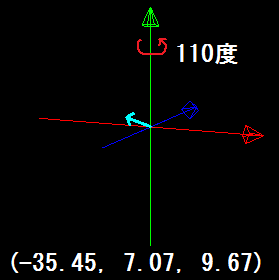
左手系座標系でＹ軸を時計回りに１１０度回転させると、(-35.45, 7.07, 9.67)になります。

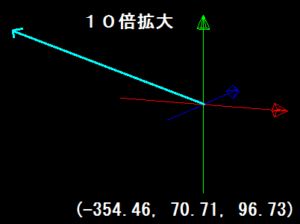
１０倍拡大すると、(-354.46, 70.71, 96.73)になります。

次に、マトリックスを使用した計算結果を見てみましょう。

変換元の行列に、ベクトル(10.0, 20.0, 30.0)を掛け合わせましょう。
-2.4184×10.0+(-2.4184×20.0)+(-9.3969)×30.0=-354.459
-7.0710×10.0+ 7.0710×20.0+ 0.0000×30.0=70.71
6.6446×10.0+ 6.6446×20.0+(-3.4202)×30.0=96.732

先程算出した計算結果と逆行列を掛け合わせると元の数値へ戻るはずです。
掛け合わせて見ましょう。
-0.0241×(-354.4612)+(-0.0707)×(70.7106)+0.0664×(96.7328)=9.96633342
-0.0241×(-354.4612)+ 0.0707×(70.7106)+0.0664×(96.7328)=19.96481226
-0.0939×(-354.4612)+ 0.0000×(70.7106)+(-0.0342)×(96.7328)=29.97564492

ほぼ元の数値へ戻りましたので、正しい逆行列を算出できているはずです。

斜めの行列に０が含まれる場合の解き方もあるのですが、逆行列に関してはここまでにしたいと思います。

２００６年頃マトリックスを使っていたので多少特性を知っていますが、今は少し忘れています。

「間違えたくない」という気持ちがあるので、コンピューターで試行して試しながら解きました。

実は、最近Youtubeに解けない数学問題があるな～とか、小学校で習う割り算の解き方を忘れていたりします。(^^;

誰が見るのかな～と思いつつ、しばらく難しい数学はお休みしましょう。(^^)

以上

前回は、右手系座標系と左手系座標系の話をしました。

今回は、回転方向についてお話したいと思います。

私は数系の人間で、数学をやっていると子供の頃は学校で式を習ります。
式を習っていくと、文章問題の壁にぶち当たります。(^^;

何れ大人になりますが、そのままでは大人として通用せず、大人になると自分で正しいことを考えられなければなりません。

何が正しいことかと言うと、実際に起こっていることが正しいことであり、現実で起こっていることを学者さん方が紐解いたものが学問だと思います。

例えば、３次元空間では図の様に軸を回転させます。
図の例は、数学的に誤った考え方であり、Ｘ軸は軸の方向へ対して反時計回り、Ｙ軸は軸の方向へ対して時計回り、Ｚ軸は軸の方向へ対して反時計回りで回転しています。

私からすると、あべこべです。

この誤った左手系座標系の回転例を元に、右手系座標系の回転方向を適当に考えると、次のように成ります。

この右手系座標系の回転方向は、左手系座標系の回転方向を真似しただけで、Ｚ方向に対しては軸の方向とは逆、つまり負の方向へ対して反時計回りしています。

この様に、まず左手座標で考えた回転方向が間違っていると、次に考える右手座標での回転方向も間違えます。
そして、左手系座標系の回転方向を真似しただけなので、右手系座標系になり軸の方向が変わった事にも気づきません。

これが数学であり、１つ間違えると後に考えた法則が間違いだらけになってしまうことがあります。

では、３次元空間での回転方向を真剣に考えると、どのようになるのか考えてみましょう。

まず、３次元には軸があり、軸には方向があります。
この方向も大切な数学的要素です。

私たちが生活をしていく上で、身の回りに有る回転するものと言えば時計です。
時計は、時計回りに回転するものです。

ですので、３次元の軸を回転させる場合は、軸の方向へ対して時計回りに回転させると理解し易いと思います。

回転させる場合、軸の方向へ対して時計回りに考えると、図の様な回転方向になります。

学校で物を習っている内は、習っていることが正しく、習っている通りに解こうとしますが、習っている事は何なのか、本当によく理解できているでしょうか？

疑問に思いますね。

例えば、ヨー・ピッチ・ロールという回転方法があるのですが、上記のように数学的な考え方をすると、回転方向に一貫性が無いことがわかります。(^^;

つまり、ヨー・ピッチ・ロールで物体を回転させる場合、Ｘ軸、Ｙ軸、Ｚ軸の回転方向を別々に暗記する、もしくは回転方向を確認しながら考えなければ成らなくなり、習っている人が理解し辛くなります。
ただし、個人的には考え方が素晴らしいと思います。(^^;

以上