一般的な月の軌道は説明が難しく、頭の良い方は簡単に理解できるのかもしれませんが、私たちにとって簡単に理解できるような説明ではないと思います。
そこで、私の視点から見た計算へ変えたいと思います。(^^;
私は、地球を水平にして太陽と月がどう動くか考えたいと思います。
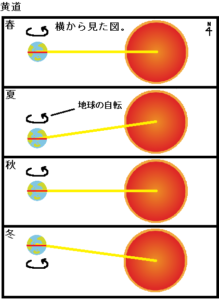
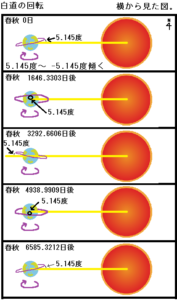
地球の赤道を赤いラインとすると、太陽、地球の関係は図の様になります。
地球は自転しています。
太陽の通り道が黄道で、赤道に対して23.44度~-23.44度の範囲に傾いています。

鼠色の矢印は、月の公転方向。
黒色の矢印は、地球の自転方向。
紫色の矢印は、白道の回転方向。
黄色の線は、黄道上にある太陽の方向で、春夏秋冬で太陽の高度が最も高くなる場所です。
紫色の曲線は、月の軌道である白道。
白道は黄道に対して、5.145度~ -5.145度の範囲に傾いています。
白道が一周する周期をサロス周期と呼び、6585.3212日で一周します。
太陽の位置を春、秋に限定した場合、この白道の軌道は、図の様に太陽へ対して傾く方向が変化し、6585.3212日(サロス周期)で一周します。
この時、地球の自転とは逆方向(紫色の矢印)へ回転して方向が変わっていく。
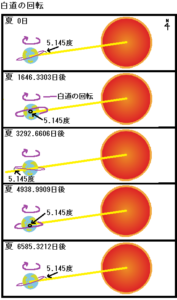
次は、太陽の位置を夏に限定した場合、白道の軌道は図の様に太陽へ対して傾く方向が変化し、図の様に白道は6585.3212日(サロス周期)で一周します。
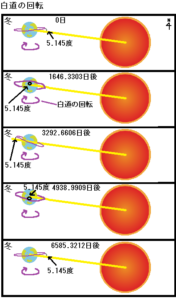
次は、太陽の位置を冬に限定した場合、白道の軌道は図の様に太陽へ対して傾く方向が変化し、図の様に白道は6585.3212日(サロス周期)で一周します。

月は楕円軌道で、地球から遠ざかったり近づいたりしながら移動しています。
※正確には、地球も月から遠ざかったり近づいたりして移動しています。
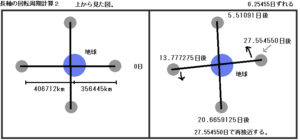
最も地球へ近づく周期は、27.554550日。
最も近づいたときの距離が、約356445km。
最も遠いときの距離が、約406712km。
この様に、月と地球の距離が周期的に変化します。

※楕円を分かり易く説明するため、誇張して表現してます。
青い線は、地球の自転。
黒い線は、楕円軌道の長軸。
オレンジ色の矢印は、長軸の回転方向。
この楕円軌道の長軸の方向は定まっておらず、緑色の矢印の方向へ3232.6054日で1周します。

紫色の線は白道。
上から見ると白道を通る月は、27.3日の周期で楕円状に地球を一周公転しています。、
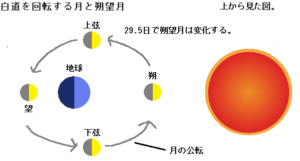
月の満ち欠け(朔望月)は、図の様に29.5日の周期で変化します。
後に説明しますが、朔望月は地球の周りを1周以上公転しています。
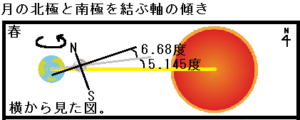
月の北極と南極を結ぶ軸は、白道に対して6.68度傾いています。
私に間違いが無ければ、これらの組み合わせにより月は動いていると習います。
さて、ここからは数学のお話です。(^^)
私が朔望月と長軸の計算をしてみたところ、地球の公転と月の公転が関係している様に思えます。
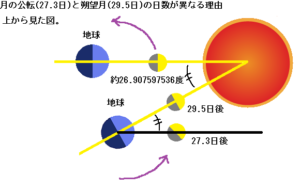
月の公転日数(27.3日)と朔望月の日数(29.5日)が違うのは、図の様に太陽の周りを公転することが理由だと思います。
月が地球を一周公転する間に27.3日経ちますので、太陽、地球、月の角度は次の角度変化します。
月が地球を公転する日数÷地球が太陽を公転する日数×360度=月が地球を公転する間に地球が太陽を公転する角度
27.3÷365.25×360.0=26.907597535934291581108829568789
適当なところで四捨五入すると、太陽を公転する角度は約26.907597536度変化することが分かります。
この時、月が太陽の方を向く日数(朔望月)を計算すると、次のような計算になります。
(月の公転角度+月が地球を公転する間に地球が太陽を公転する角度)÷月の公転角度×月の公転日数=朔望月に近い日数
(360.0+26.907597536)÷360.0×27.3=29.340492813146666666666666666667
適当なところで四捨五入すると、約29.340493日。
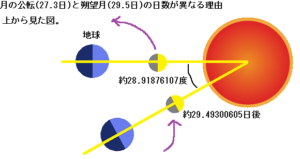
29.340493日-27.3日=2.040493なので、約2日進んだ事になります。
進んだ分、再計算しなければなりません。
29.340493÷365.25×360.0=28.918761067761806981519507186858
(360.0+28.91876107)÷360.0×27.3=29.493006047808333333333333333333
適当なところで四捨五入すると、約29.49300605日。
月が太陽の方へ向くまでの日数は約29.49300605日になり、やはり朔望月に近い日数になります。
次に、長軸の周期も同様に算出することが出来そうなので、計算してみます。
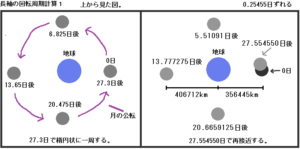
月の公転周期と近点周期(月が地球へ再接近する周期)を同じ時間軸で並べると、図の様になります。
つまり、月が最も地球に近づいたときから、次に月が近づいてくるまでの間に、月が少し公転しているということになります。
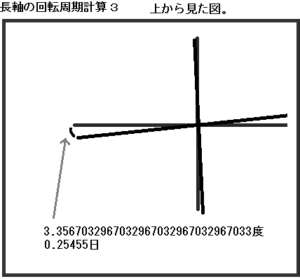
ずれが一周するまでの日数を計算すると、次のように成ります。
(月の近点周期-月の公転周期)=近点周期と公転周期の差
27.554550-27.3=0.25455日
1度の公転により、0.25455日遅れて月が地球へ近づくことが分かります。
近点周期と公転周期の差÷公転周期×360.0=ずれる角度
0.25455÷27.3×360.0=3.3567032967032967032967032967033度
1度の公転で、約3.3567032967032967032967032967033度ずれることが分かります。
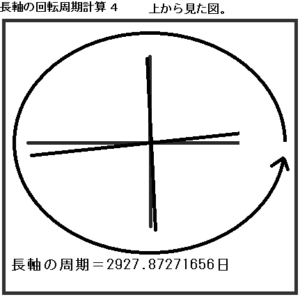
360度÷ずれる角度×公転周期=長軸が一周する周期(日数)
360.0÷3.3567032967032967032967032967033×27.3=2927.872716558632
ずれる角度が一周する日数と、この間に公転した日数により、長軸が回転しそうな角度を算出しています。
適当なところで四捨五入すると、長軸の回転周期は2927.87271656日となります。
インターネットに掲載されている月の長軸の回転周期は3232.6054日なので、間違っているかも知れませんね。(^^;
理解するまで苦労しましたが、未だに理解できていないように思えますが・・・。(^^;
学問として伝わっている月のお話なので、数値を参考にしているのですが、人と同じ内容を書くと間違いまで真似てしまいますので、自分で考えて説明しています。
間違っているかもしれませんので、参考程度に見てください。 (^^;
以上