世の中には、簡単な事のようでよく理解できていない事が多くあります。
その1つが数の数え方であり、小学生の頃に習う算数でさえ、よく理解できていないことがあります。
日頃、高等な数式を覚えると共に、難易度の高い数式を解くことが凄いように感じるでしょうが、高度な数式を覚える前にしっかりとした基礎を築くことはとても大切なことです。
基礎がしっかしりていなければ、応用も雑に認識したり、つじつまを合わせるようになります。
私がプログラムを覚えたばかりの頃に悩んだ事なのですが、一般的な数値計算には正解と間違いがあり一貫性がない場合がありません。
これから、その中の1つを証明してみようと思います。

これは時計の計算ですが、時間を計算するとき、0時から始まり、5分、15分、30分、45分、そして60分立つことで1時になります。
そして、0時、3時、6時、21時と時間が過ぎ、24時になると次の日へ移り変わります。
この計算は、数学的に正しいと思います。
1月1日、1月2日、1月3日、1ヵ月後は2月になります。
時計は0時から始まるのですが、カレンダーは1月から始まります。
これについては、間違っていると思います。
まだ、1ヶ月経っていないのに1月と呼んでいます。
当たり前の事と思うでしょうが、これがおかしいのです。
何故おかしいか、ドーナッツを例に挙げて説明したいと思います。

これを4等分します。
すると、4つドーナッツの欠片が出来ました。
この時、ドーナッツを1とすると、欠片1つは4分の1の大きさになります。
個数で言うと、0.25個のドーナッツです。
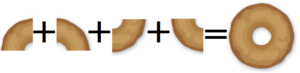
0.25個のドーナッツを4つ足すと、1つのドーナッツになります。
算数では、0.25個のドーナッツを1とは数えません。

カレンダーに戻って説明すると、1月の1日、2日、3日、4日、5日は、まだ1カ月経っていないのに1月と計算しています。
1月は31日ありますが、まだ31日経っていないのに1月とカウントしています。
これは、ドーナッツの例で言うのならば、4等分した1欠けら、0.25個のドーナッツを1個のドーナッツと計算しているような物です。

時計で例えるのならば、0時30分を1時30分と呼ぶようなものです。
まだ30分しか経っていないのに、1時30分とは計算しません。
よく考えてみてください。
12ヶ月あるうちの12月は、12分の12。
12分の12=1年
分数を解くと、12月は既に1年経っているということになります。
正しい計算例を挙げたいと思います。
1.時間計算。0時~23時59分99秒の様に計算します。24時は次の日です。
2.年齢計算。0才から始まり、1年経つと1才になります。
間違った計算例を挙げたいと思います。
1.月の計算。1月~12月。
2.西暦の計算。1年~2019年。
3.世紀の計算。1世紀から21世紀。
数え方に一貫性がないというところから考えると、多分、数え方をよく理解できていません。
これは推測ですが、多分大学を卒業していても、この様な数の数え方を理解できずに生きています。
間違いを正しますと、次のような計算になります。
1.月の計算。
0月から始まり11月で終わる。
2.西暦の計算。
0年から始まります。
3.世紀の計算。
0世紀から始まります。
4.年と世紀を計算すると、0年~99年=0世紀。100年~199年=1世紀。
この様に修正すると、次のような計算になります。
西暦は、0世紀0年0月0日0時に始まります。
24時間経つと、0世紀0年0月1日0時になります。
1月31日ではなく、1月は0~30日までなので、31日は次の日になります。つまり、0世紀0年1月0日0時になります。
12月ではなく、0世紀1年0月0日0時になります。
100年経つと、1世紀0年0月0日0時になります。
つまり、時間は0時から始まり、24時になると次の日へ移り変わります。
0月は0日から始まり、30日で終わります。31日は次の月です。
年は0月から始まり11月で終わる。12月は次の年です。
世紀は0年から始まり99年で終わる。100年は次の世紀です。
何故、私がこの様に考えるかと言うと、年を日付へ変換するとき、次のような計算になるのです。
(年-1)÷4+(年-1)*365=日数
この時うるう年(年÷4)は、365×4+1=約1461日を4年で割ると365.25になるので、1年に1度日付を修正することで端数を出さないように計算していると思っています。
ですが、式の中で-1はつじつまを合わせるため、西暦では0年がないのでうるう年を1つ引いています。
そこで、おかしいと思ったんですね。
算数では0から始まるので、年を計算するならば0年から始まります。
年を世紀の単位へ変換すると、次のように成ります。
0.00世紀=0年
0.01世紀=1年
0.02世紀=2年
0.99世紀=99年
1.00世紀=100年
これが算数だと思います。
基礎を間違えると応用も間違いだらけになったり、曖昧にして誤魔化す事もありますので、基礎はとても大切です。
簡単なことだと軽視してはなりません。
そして、実は簡単なようで多くの方が理解できていない難しい基礎計算だと思います。
勿論、私の個人的な意見であり、私が正しかったとしても変える必要はありません。(^^;

