コマが倒れるまでを分析

次の記事は、今回のお話に関連するお話です。
１．だるまが起き上がる仕組みを分析
２．コマが倒れるまでを分析
３．自転車がバランスよく進む仕組みを分析

今回は、次の物理法則に関する概念を加えたいと思います。
４．質量中心と浮心、幾何中心について
５．船が海に浮く時のバランス計算
６．重心と質量中心、浮心について

世の中にある知識を基にした私の推論であることを、予めご了承ください。

今回はコマが何故倒れることなく回り続けるかを考えてみましたが、少し難しいので自信がありません。
また厄介な事を考えてしまった・・・と思ってます。(^^;

たぶん、コマの重心は図の辺りだと思います。

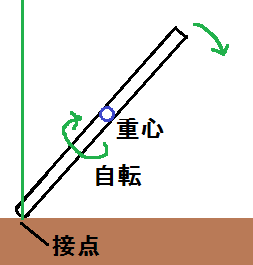
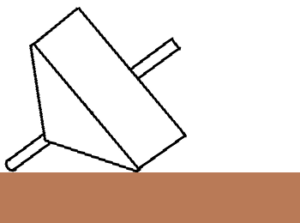
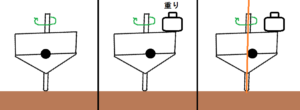
もし仮にコマが棒だけならば、動いていない状態でも、自転していていたとしても、図の様に右へ倒れます。

コマは、自転していない状態で図の様に傾くと右側へ倒れます。

コマは、図の様に中央が大きくなければ安定して回転することが出来ませんし、回転していなければ倒れます。
何故、中央が大きくなければ安定して回転しないのか・・・と考えると、私は「遠心力が関係あるのではないか？」という結論に到りました。

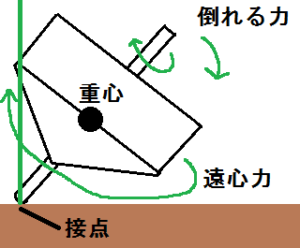
例えば、図の様に時計回りにコマを回転させたとします。
すると、右側へ倒れようとします。

ですが、コマは上から見ると時計回りに自転しています。

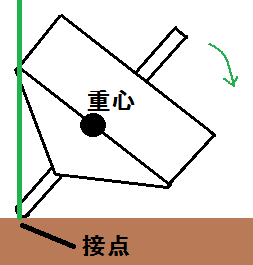
この時、自転による遠心力は、コマの中心からコマの軸（オレンジ色のライン）を中心として、コマの回りには遠心力が働いています。
遠心力は、コマの軸から遠いほど力が働きますので、コマの中央部分が広ければ広いほど、大きな遠心力が働きます。

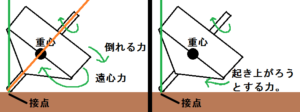
この遠心力が掛かる部分ですが、接点を中心に物体が傾こうとするとき、遠心力の掛かる部分が右側へ倒れようとします。
この時、オレンジ色の軸から右にある部分は、倒れる力に加えて遠心力が働きます。

この力を合わせると、右図の様なコマが右回転に起き上がろうとする力へ変わります。

難しいですよね？
もう少し細かく考えてみましょう。

例えば、回転中に重りを載せるとどうなるでしょう。
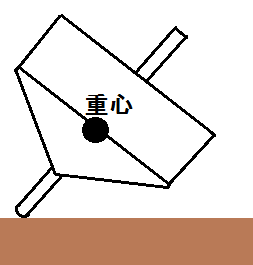
重心がずれたので遠心力が働きバランスを崩します。
この時、私はオレンジ色のラインを中心として回転していた物体の重心が右側へ偏り、遠心力によりバランスを崩していくと思っています。

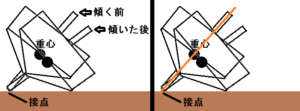
時間を含めてコマがどのように動いているのか考えてみましょう。

回転中のコマは常に倒れようとしているはずです。
図の様に、傾く前のコマと傾いた後のコマとでは重心が図の様に変化します。

この時、オレンジ色のラインを中心に回転していたコマの中心が、右図の様にずれるということに成ります。

このずれた重心へ円引力が働くと、コマは起き上がろうとすると思うんですね。

この様に考えると、コマは倒れそうになるのですが、時計回りへ起き上がろうとするので、時計回りにこけないような回り方をします。

まとめて説明すると、コマを時計回りに回転させると、時計回りへ自転しながら、時計回りにこけないように回ります。

ですので、コマは倒れることなく回転し続けます。

やがてコマの回転する力が衰えると共に遠心力が得られなくなり、倒れる力が勝るようになると、徐々に大きく傾きながら倒れます。

この様に、私は独学ですが物理現象を考えています。
物理の計算が得意と言うわけではありませんから、学校で習う細かな物理計算は知りません。(^^;

私がブログに載せている気象関係のお話は、物体の運動と熱力学を応用しています。

勿論、今回の話も私の推測ですので、間違っているかも知れません。

暇つぶしに考えているだけなので、面倒な計算をする気はありません。(^^;