３次元空間の回転方向とおかしな例

前回は、右手系座標系と左手系座標系の話をしました。

今回は、回転方向についてお話したいと思います。

私は数系の人間で、数学をやっていると子供の頃は学校で式を習ります。
式を習っていくと、文章問題の壁にぶち当たります。(^^;

何れ大人になりますが、そのままでは大人として通用せず、大人になると自分で正しいことを考えられなければなりません。

何が正しいことかと言うと、実際に起こっていることが正しいことであり、現実で起こっていることを学者さん方が紐解いたものが学問だと思います。

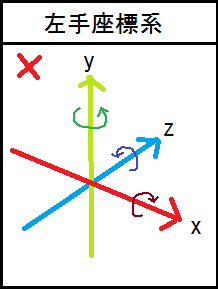
例えば、３次元空間では図の様に軸を回転させます。
図の例は、数学的に誤った考え方であり、Ｘ軸は軸の方向へ対して反時計回り、Ｙ軸は軸の方向へ対して時計回り、Ｚ軸は軸の方向へ対して反時計回りで回転しています。

私からすると、あべこべです。

この誤った左手系座標系の回転例を元に、右手系座標系の回転方向を適当に考えると、次のように成ります。

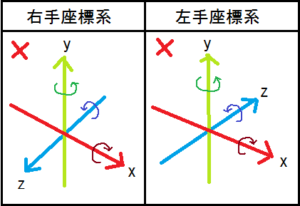
この右手系座標系の回転方向は、左手系座標系の回転方向を真似しただけで、Ｚ方向に対しては軸の方向とは逆、つまり負の方向へ対して反時計回りしています。

この様に、まず左手座標で考えた回転方向が間違っていると、次に考える右手座標での回転方向も間違えます。
そして、左手系座標系の回転方向を真似しただけなので、右手系座標系になり軸の方向が変わった事にも気づきません。

これが数学であり、１つ間違えると後に考えた法則が間違いだらけになってしまうことがあります。

では、３次元空間での回転方向を真剣に考えると、どのようになるのか考えてみましょう。

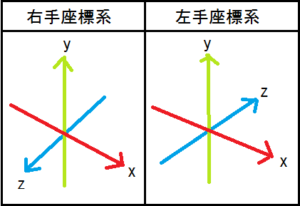
まず、３次元には軸があり、軸には方向があります。
この方向も大切な数学的要素です。

私たちが生活をしていく上で、身の回りに有る回転するものと言えば時計です。
時計は、時計回りに回転するものです。

ですので、３次元の軸を回転させる場合は、軸の方向へ対して時計回りに回転させると理解し易いと思います。

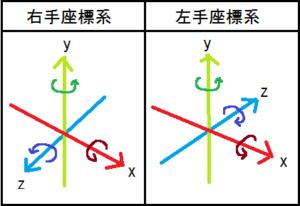
回転させる場合、軸の方向へ対して時計回りに考えると、図の様な回転方向になります。

学校で物を習っている内は、習っていることが正しく、習っている通りに解こうとしますが、習っている事は何なのか、本当によく理解できているでしょうか？

疑問に思いますね。

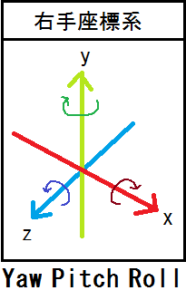
例えば、ヨー・ピッチ・ロールという回転方法があるのですが、上記のように数学的な考え方をすると、回転方向に一貫性が無いことがわかります。(^^;

つまり、ヨー・ピッチ・ロールで物体を回転させる場合、Ｘ軸、Ｙ軸、Ｚ軸の回転方向を別々に暗記する、もしくは回転方向を確認しながら考えなければ成らなくなり、習っている人が理解し辛くなります。
ただし、個人的には考え方が素晴らしいと思います。(^^;

以上