確率通りになるまでの試行回数、パチンコ・パチスロ・投資の統計的確率

投資ではボリンジャーバンド、賭け事ではパチスロのボーナス確率等、賭け引きをする上で確率を扱うことが多いと思います。
大雑把ですが確率を算出するプログラムを作りましたので、賭け事や投資をする上で避けて通ることが出来ない確率について調べたいと思います。

例えば、パチスロでＢＩＧボーナスの確率が３００分の１だとします。
実際、１０００回転させても３００分の１にはなり難いことを証明したいと思います。

実は確率には２つの種類があります。
１つは必ず確率通りに当選する確率、もう１つは確率通りに当選しない確率です。
＃これらには名前が付いていたはずですが、インターネットで探したけど見つかりませんでした。

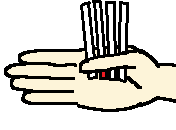
これは４個の中に必ず１つの当たりがある確率で、４分の１です。
４個引くと必ず当たりが出ますが、当たりは１つしかありません。

サイコロを使用し１を当たりとして抽選すると、６個中１個に当たりがあるので、６分の１です。
この場合、６回転がしても１が出ない場合があったり、６回とも１になることがあります。

パチスロはサイコロと同じ原理で、レバーを押す度に役を抽選しています。
以前調べた情報によりますと、「ノーマル機でボーナスの確率が３００分の１ならば、レバーを押す度に３００分の１でボーナスを抽選する」と聞いています。

では、サイコロの様に抽選し、３００分の１の統計的確率になるまで、どれぐらいレバーを押したらいいか検証してみましょう。
検証には、メルセンヌ・ツイスタ ライブラリによる乱数から、統計的確率算出したいと思います。

※理論的確率　前述したくじやサイコロの様な数学的に算出した確率を理論的確率といいます。
※統計的確率　実際サイコロを振り、出現数から算出した確率を統計的確率といいます。

ソースコード
2021-02-43.cpp
 
上記のプログラムにより簡単なテストをし、次のような結果が出ました。

試行回数	当選数	試行結果	統計的確率	ファイル
１０００回転×１０回	BIG=2, 1, 3, 2, 2, 5, 0, 0, 5, 1 REG=4, 4, 1, 2, 3, 4, 5, 3, 5, 3	BIG=21 REG=34	BIG=1/476 REG=1/294	2021-02-45
１万回転×１０回	BIG=39, 34, 20, 39, 30, 30, 40, 20, 29, 30 REG=56, 49, 49, 51, 49, 43, 40, 50, 60, 41	BIG=311 REG=488	BIG=1/321 REG=1/204	2021-02-46
１０万回転×１０回	BIG=329, 349, 352, 371, 329, 358, 336, 336, 357, 358 REG=520, 561, 515, 515, 490, 546, 505, 486, 477, 513	BIG=3475 REG=5128	BIG=1/287 REG=1/195	2021-02-47
５０万回転×１０回	BIG=1686, 1708, 1709, 1707, 1733, 1647, 1661, 1743, 1682, 1663 REG=2476, 2572, 2528, 2536, 2469, 2448, 2561, 2440, 2566, 2494	BIG=16939 REG=25090	BIG=1/295 REG=1/199	2021-02-48
１００万回転×１０回	BIG=3400, 3287, 3434, 3329, 3398, 3334, 3425, 3384, 3337, 3284 REG=4977, 5077, 4824, 5076, 4963, 4972, 5091, 4935, 5143, 4956	BIG=33612 REG=50014	BIG=1/297 REG=1/199	2021-02-49

※４号機、ノーマルＡタイプで仮定して試行。
※ＢＩＧは３００分の１で当選。
※ＲＥＧは２００分の１で当選。
※回転数×１０回を１０回試行し、ＢＩＧとＲＥＧの理論的確率と統計的確率の差が最も大きい試行結果を載せています。

大雑把な計算ですが、３００分の１、２００分の１といった理論的確率に近くなる試行回数（回転数）は、図の様になります。
１０万回転×１０回で、ＢＩＧとＲＥＧの確率と統計的確率の分母が１３前後違う。
５０万回転×１０回で、ＢＩＧとＲＥＧの確率と統計的確率の分母が５前後違う。
１００万回転×１０回で、ＢＩＧとＲＥＧの確率と統計的確率の分母が３前後違う。

このように、３００分の１で５００万回～１０００万回程試行しなければ、理論的確率と統計的確率の間に大きな誤差が生じます。
つまり、１０００回程度ならば３００分の１になり難いということです。

今回は、メルセンヌ・ツイスタ ライブラリを使用して出た結果なので、このライブラリを使用することにより、統計的確率が理論的確率通りになるかを試したに過ぎません。
ですが、基本的には相当な回数試行しなければ、統計的な確率と理論的な確率は近い数値にならないと思います。(^^;

以上