月蝕により月が完全に地球に隠れるかを計算

今回は、月蝕により月が完全に隠れるかどうかを計算してみたいと思います。

隠れるといっても、地球の大気により光が屈折し、弱い光により赤く見えるので、完全に見えなくなるということではありません。

私は図形が苦手なのですが、今回は苦手な図形の計算を使って月蝕を説明したいと思います。

月のデータは、次のようになっています。

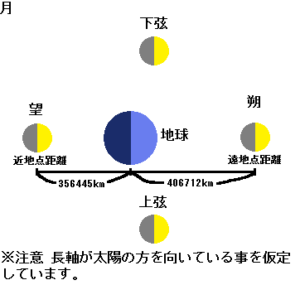
近点距離	356445km
遠点距離	406712km
直径	3474.3km

地球のデータは、次のようになっています。

赤道の直径	12756.274km
極半径	6356.752km
極直径	12713.504km

太陽のデータは、次のようになっています。

直径	1392000km
半径	696000km
距離	147100000km～152100000km

---

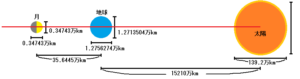
太陽の距離を152100000kmとして、これを図で表すと、次のように成ります。

※大雑把に描いたので、正確な図ではありません。

月は地球に近いほど地球の陰に隠れ易いので、近点距離を使用しています。

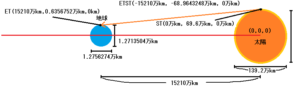
まず、太陽の中心を基点として計算してみましょう。
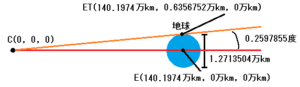
地球の上部をETとし、座標を計算すると、ET(15210万km, 0.6356752万km, 0km)になります。
太陽の上部をSTとし、座標を計算すると、ST(0万km, 69.6万km, 0万km)になります。
ETとSTを結んだラインをETSTとし、ETSTベクトルは(-15210万km, -68.9643248万km, 0万km)になります。

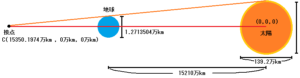
オレンジのベクトルと赤いラインとが交わる点をCとし、CはETSTベクトルの高さが0万kmに達したとき接点へ到達しますので、座標を算出すると、次のように成ります。

15210.0×69.6÷68.9643248=15350.197411053316076256284901668
適当なところで四捨五入すると、15350.1974万kmになります。

つまり、太陽を基点としたＣの座標は、次のように成ります。
C=(15350.1974万km, 0万km, 0万km)

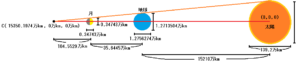
月から接点までの距離は、15350.1974-15210.0-35.6445=104.5529。
近距離地点に月がある場合、接点から月までの距離が、104.5529万kmということが分かります。

分かり易くするため、次は接点から座標を計算してみましょう。

月の座標をM、月の上部をMT、地球の座標をE、地球の上部をETで表しています。
M(104.5529万km, 0万km, 0万km)
MT(104.5529万km, 0.173715万km, 0万km)
E(140.1974万km, 0万km, 0万km)
ET(140.1974万km, 0.6356752万km, 0万km)

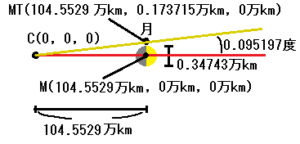
まず、接点(C)から月の上部(MT)を結ぶラインと、接点(C)から太陽(S)を結ぶラインの角度を求めたいと思います。

懐かしい式ですよね。

M(104.5529万km, 0万km, 0万km)
MT(104.5529万km, 0.173715万km, 0万km)

まず、Mの距離を求めましょう。
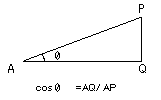
AQ=sqrt(104.5529×104.5529+0×0+0×0)=104.5529

まず、MTの距離を求めましょう。
AP=sqrt(104.5529×104.5529+0.173715×0.173715+0×0)=104.55304431393293963514878348274

acos(AQ÷AP)×180.0÷3.141592が角度になりますので、数値を当てはめてみるます。、

acos(104.5529/104.55304431393293963514878348274)*180.0/3.141592
=0.09519704550782894708944529026672
適当なところで四捨五入すると、0.095197度になります。

結果、月(M)と月上部(MT)の角度は、0.095197度になります。

2022-09-09.PNG

E(140.1974万km, 0万km, 0万km)
ET(140.1974万km, 0.6356752万km, 0万km)

まず、Eの距離を求めましょう。
AQ=sqrt(140.1974×140.1974+0×0+0×0)=140.1974

まず、ETの距離を求めましょう。
AP=sqrt(140.1974×140.1974+0.6356752×0.6356752+0×0)=140.1988411140402224401941656058

acos(AQ÷AP)×180.0÷3.141592が角度になりますので、数値を当てはめてみるます。、

acos(140.1974÷140.1988411140402224401941656058)×180.0÷3.141592
=0.25978553464019836892337085193357
適当なところで四捨五入すると、0.2597855度になります。

結果、地球(E)と地球上部(ET)の角度は、0.2597855度になります。

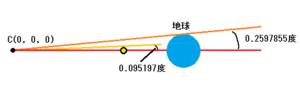
太陽と地球の距離が152100000kmの時、接点から見た太陽と月上部の角度0.095197度に対し、太陽と地球上部の角度は0.2597855度なので、完全に地球の影に隠れると思います。

---

次は、太陽の距離を147100000kmとして計算してみましょう。
これを図で表すと、次のように成ります。

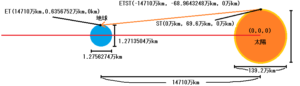
太陽の中心を基点として計算してみましょう。
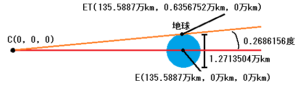
地球の上部をETとし、座標を計算すると、ET(14710万km, 0.6356752万km, 0km)になります。
太陽の上部をSTとし、座標を計算すると、ST(0万km, 69.6万km, 0万km)になります。
ETとSTを結んだラインをETSTとし、ETSTベクトルは(-14710万km, -68.9643248万km, 0万km)になります。

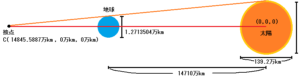
オレンジのベクトルと赤いラインとが交わる点をCとし、CはETSTベクトルの高さが0万kmに達したとき接点へ到達しますので、座標を算出すると、次のように成ります。

14710.0×69.6÷68.9643248=14845.588686166619295314263701745
適当なところで四捨五入すると、14845.5887万kmになります。

つまり、太陽を基点としたＣの座標は、次のように成ります。
C=(14845.5887万km, 0万km, 0万km)

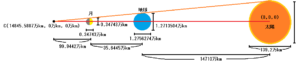
月から接点までの距離は、14845.5887-14710.0-35.6445=99.9442。
99.9442万kmということが分かります。

分かり易くするため、次は接点から座標を計算してみましょう。

月の座標をM、月の上部をMT、地球の座標をE、地球の上部をETで表しています。
M(99.9442万km, 0万km, 0万km)
MT(99.9442万km, 0.173715万km, 0万km)
E(135.5887万km, 0万km, 0万km)
ET(135.5887万km, 0.6356752万km, 0万km)

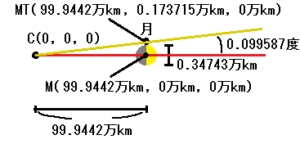
まず、接点から月の上部(MT)を結ぶラインと、接点から太陽(E)を結ぶラインの角度を求めたいと思います。

M(99.9442万km, 0万km, 0万km)
MT(99.9442万km, 0.173715万km, 0万km)

まず、Mの距離を求めましょう。
AQ=sqrt(99.9442×99.9442+0×0+0×0)=99.9442

まず、MTの距離を求めましょう。
AP=sqrt(99.9442*99.9442+0.173715*0.173715+0×0)=99.944350968632664386484886256899

acos(AQ÷AP)×180.0÷3.141592が角度になりますので、数値を当てはめてみます。、

acos(99.9442÷99.944350968632664386484886256899)×180.0÷3.141592
=0.09958683260382927326549595475813
適当なところで四捨五入すると、0.099587度になります。

結果、月(M)と月上部(MT)の角度は、0.099587度になります。

E(135.5887万km, 0万km, 0万km)
ET(135.5887万km, 0.6356752万km, 0万km)

まず、Eの距離を求めましょう。
AQ=sqrt(135.5887×135.5887+0×0+0×0)=135.5887

まず、ETの距離を求めましょう。
AP=sqrt(135.5887×135.5887+0.6356752×0.6356752+0×0)=135.59019009740304601133993037296

acos(AQ÷AP)×180.0÷3.141592が角度になりますので、数値を当てはめてみます。、

acos(135.5887÷135.59019009740304601133993037296)×180.0÷3.141592
=0.26861559450725413884032304233341
適当なところで四捨五入すると、0.2686156度になります。

結果、地球(E)と地球上部(ET)の角度は、0.2686156度になります。

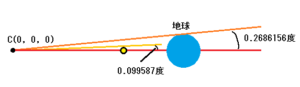
太陽と地球の距離が147100000kmの時、接点から見た太陽と月上部の角度0.099587度に対し、太陽と地球上部の角度は0.2686156度なので、完全に地球の影に隠れると思います。

私は自信家ではないので、常に「間違っているかもしれない」と思っています。
間違っていたらはずかしい、はずかしいけどやってみたくなるわけです。(^^;

今回は、月が地球に隠れるかを計算してみました。

以上