私は数系で、立体空間での計算をしています。
私は3D計算をする際、左手系座標系で計算します。
右手系座標系は難しいと思うんですね。

2020-11-21.png
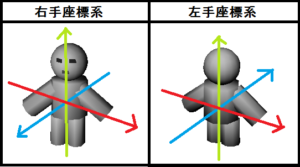
図は、右手系座標と左手系座標の違いです。
2020-11-22.png
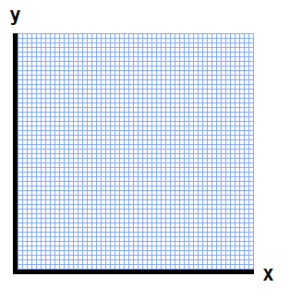
これは、皆さんが学校で習う2次元の図形です。
先ほどの図を見ると分かるのですが、右手系座標のZ軸は手前がプラス、左手系座標のZ軸は奥がプラスになります。
アニメーションさせる際、物体を前進させようとすると、右手系座標系は手前へ移動し、左手系座標系では奥へ移動します。
私は、頭の中でイメージするとき、自分の向きと物体の向きが同じ場合、考え易い。
右手系座標系の様に、物体が手前へ向いている場合、物体をZ軸のプラス方向へ移動させると、物体は手前へやってくる。
右手系座標系で物体を右へ移動させたいと思う場合、X軸のマイナス方向へ移動させなければ成らない。
右手系座標系で物体を左へ移動させたいと思う場合、X軸のプラス方向へ移動させなければ成らない。
これが、とても厄介なんです。
右手系座標系と左手系座標系で前後が逆なので分かり難いでしょう。
ですので、Y軸を180度回転させて同じ方向にしてみましょう。
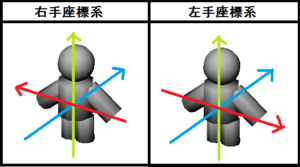
すると、図の様に右手系座標系では左右が反対になる事がわかります。
つまり、右手系座標系で右へ進もうとすると、X軸のマイナス方向へ移動させなければならない。
右手系座標系で左へ進もうとすると、X軸のプラス方向へ移動させなければならない。
これは、物体を製作するときも同じだと思います。
3次元計算を教える上で、右手系座標系は難しい覚え方だと思います。
以上。