モンティホール問題は、天才マリリン・ボス・サヴァントが正解し、数学者が間違えた問題です。
今回は、モンティホール問題の簡単なトリックについて、お話をしたいと思います。
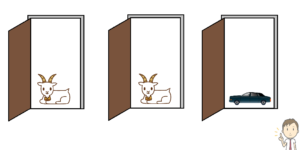
司会者モンティがいて、ドアが3つあり、3つの中に1つだけ後ろに新車がある。
残りのドアは、後ろにヤギがいる。
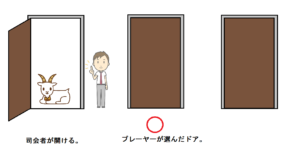
司会者モンティは、残りのドアからやぎが入っているドアを必ず1つ開ける。
司会者モンティは、プレイヤーにドアを選び直してよいと言う。
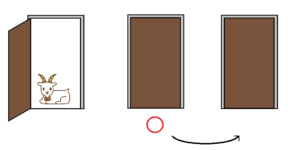
2021-08-04.png
ここでドアを選び直し、閉まっているドアの内、選んだドアではない方を選ぶと、確立が3分の2になります。
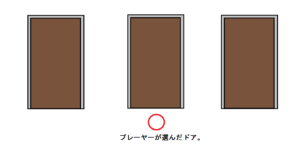
これは簡単なトリックなのですが、プレイヤーが3つのドアから1つ選んだ時点では、正解確率は3分の1です。

司会者モンティは、プレイヤーが選んだドア以外からヤギの入っているドアを開けます。
すると、閉まったドアは車とヤギが隠れています。
つまり、当たりと外れのドアが残ります。
当たりと外れのドアを入れ替えると、正解と不正解が入れ替わります。
つまり、ドアを選び直す事で、正解する確率が3分の1から3分の2へ変わります。
外れを選ぶ場合の手順を追ってみましょう。
1.始めに3分の2で外れを引いた。
2.当たりと外れを入れ替えると、当たりになる。
当たりを選ぶ場合の手順を追ってみましょう。
1.始めに3分の1で当たりを引いた。
2.当たりと外れを入れ替えると、外れになる。
Wikipediaには、ドアを100個増やした例を説明していますが、我々一般人にとってドアの数が増えるとより複雑になり混乱します。(^^;
頭のいい人ならば、ドアが100個に増えても問題ないかも知れませんが・・・。
数は少ない方が理解し易いと思います。
さて、数学者が間違え、天才が正解した問題です。
当然、私も数系なので適当に確率を当てはめて間違た様な覚えがありますw
Wikipediaの説明を見ると100個のドアがどうのこうの書いているので、私は「考えるのが面倒だ」と思っていました。(^^;
どちらが正しいことを言っているのか分かりませんでしたので、コンピューターでシミュレーションして確認し、本当の話だったので、細かいところまで考えて分析することにしました。
以上
