重心と質量中心、浮心について

次の記事は、今回のお話に関連するお話です。
１．だるまが起き上がる仕組みを分析
２．コマが倒れるまでを分析
３．自転車がバランスよく進む仕組みを分析
４．質量中心と浮心、幾何中心について
５．船が海に浮く時のバランス計算

今回は、次の物理法則に関する概念を加えたいと思います。
６．重心と質量中心、浮心について

このお話は、次のお話も関係しています。
１．月蝕により月が完全に地球に隠れるかを計算
２．月の軌道

今回は、重心と質量中心、浮心について考えてみましょう。

私の考えなので、間違いがあることを前提として見た方がいいでしょう。

まず、質量中心は重さの中心であり、重さの偏りを示している。
地球上の一様な重力下では、重心と質量中心は同じです。
同様に、浮心は浮力の中心であり、浮力の偏りを示すものです。

 

まず、浮力とは水中で水より軽い物体に働きます。

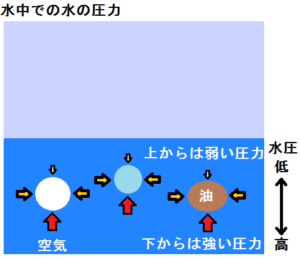
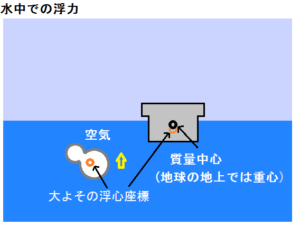
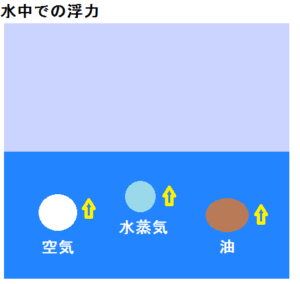
例えば、水中では図の様に軽い物体は重い水の圧力により、上へ押し出されるように浮上していきます。
水中で軽い物が上へ押し出される理由は、水深が深いほど圧力が高いので下からの圧力は強くなり、水深が浅いほど圧力が低いので上からの圧力は弱くなり、下からの強い圧力が優勢になり押し出されるわけです。

 

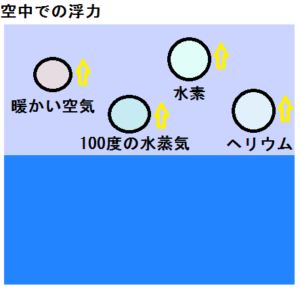
実は、空中でも空気より軽い物体に対して浮力が働きます。
この時、周囲には重い物体である空気があります。

つまり、浮力と言うのは周囲の物質より軽いものに働く力です。

 

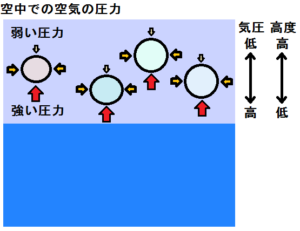
空中では、空気の圧力が各気体へ掛かり、上へ押し出されるように浮上していきます。
空中でも同じく、高度が高い場所ほど気圧が低く、高度が低い場所ほど気圧が高いので、下からの圧力が強くなり、上からの圧力は弱くなることで、上へ押し出されていきます。

これが、浮力の正体ですね。
次は、何処でどのように浮力が働くかを考えてみましょう。

 

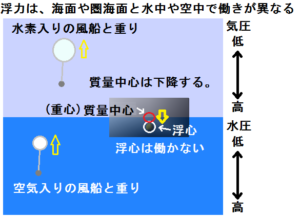
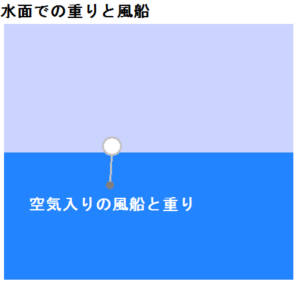
例えば、図の様に風船と重りがあったとすると、これら軽い物質は中、つまり水中や空中にあるので、圧力により上へ押し出されることで浮上していきます。

ただし、それは中であって、海中や空中では浮上しますが、海面や圏海面（対流圏海面、成層圏海面など）では、そこを境に組成が異なるので、浮上していくと周囲の物体の方が軽くなります。

 

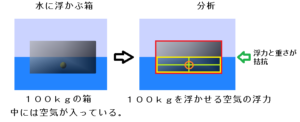
例えば、海面というのは空気と水の境目です。
空気や水よりも重い箱の重心は下降し、水よりも軽い箱の中の空気は浮上しようとします。

しかし、物体は上昇することが出来ません。
何故かと言うと、海面では重さと浮力がつり合っているので、これ以上、物体は浮上出来ないからです。

浮力の影響を強く受けることがあるとすれば、箱が沈む場合です。

 

例えば、図の様に風船と重りが水面に浮かんでいたとします。

風船は軽いので、重りに引っ張られて横へ移動しようとします。
重りは水よりも重たいので、風船と重りがつり合っている場所（赤いライン）から下へ落下しようとします。

 

すると、図の様になりますね。

---

では、重心について考えてみましょう。

質量中心と重心は異なるわけですが、一様な重力下、つまり地球の地上などは一様の重力が掛かるため、質量中心と重心が同じです。

では、一様ではない重力下とは、どのような状況でしょう？

 

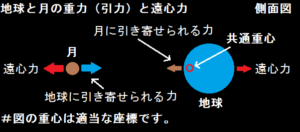
＃図の重心は適当な座標です。
例えば、地球は月の重力により引っ張られ、月は地球の重力により引っ張られ、お互いに遠心力が掛かっている状態だと思います。
複数の重力元がある場合、図の様に物体へ掛かる重力は複数あるので、互いに引っ張りあうことになる。
地球と月は、重心を中心として回転しています。
月は重心から離れているため、大きな遠心力が働き、質量の大きな地球の重力に強い力で引っ張られている。
地球は重心に近いので、小さな遠心力が働き、質量の小さな月の重力に弱い力で引っ張られている。

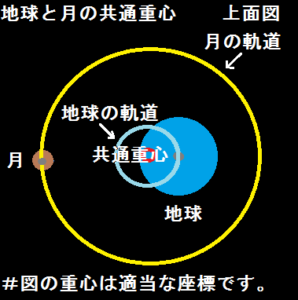
＃図の重心は適当な座標です。
この２つは重心を中心としてお互いに回転しています。

地球は、重心を中心として地球の中心は水色の円で表す軌道で回転しています。
月は、重心を中心として月の中心は黄色の円で表す軌道で回転しています。

これが重心だと思います。
＃間違っているかもしれませんよ。(^^;

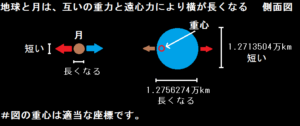
＃図の重心は適当な座標です。
そして、月は常に同じ方を向くので、地球と月は、互いの重力と遠心力により横長になるのかも知れませんね。

---

私は空間計算が専門分野なので、私なりに共通重心の位置を計算して見ましょう。
＃勿論、一般的に言われている共通重心とは位置が違います。

地球と月は、共通重心を回転しているので、共通重心は静止している状態（静的）な共通重心と動いている（動的）な共通重心がある。
ここでは、動的なものを動的共通重心とし、平均的な距離を考えてみたいと思います。

簡単な軌道から大よその相対的な動的共通重心を割り出すことができると思うのですが、次に挙げる月のデータを使ってみようと思います。

月の近点距離	356445km
月の遠点距離	406712km
月の直径	3474.3km

月の近点距離は、地球と月が最も近づく距離。
月の遠点距離は、地球と月が最も離れる距離。
これらの距離は、太陽系の状況により距離が変化する可能性があります。

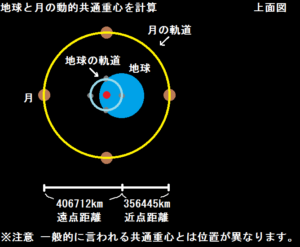
これを合成すると、図の様に月は地球から遠ざかったり離れたりしていることが考えられるので、月と地球に近点距離と遠点距離があることも説明が付く。
つまり、動的共通重心を公転する速度は、地球と月で異なるのではないかと考えてしまいます。

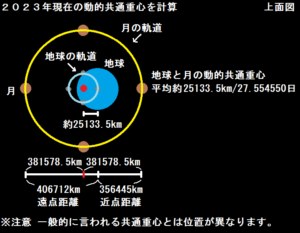
(406712km+356445km)÷2=381578.5km
406712km-381578.5km=25133.5km

つまり、地球の中心から約25133.5kmの地点に動的共通重心がありそうです。

月は、図の様に地球へ近づいたり離れたりしますので、27.554550日毎に地球へ近づく。

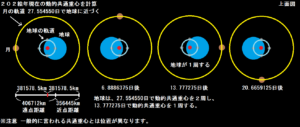
つまり、図の様に地球は13.777275日で動的共通重心を１周し、27.554550日で２周する。
月は、27.554550日で動的共通重心を１周する。

このように考えると、地球と月の動的共通重心の座標は27.554550日平均で地球の中心から約25133.5km地点にある可能性があるということになり、近点距離と遠点距離がある理由も説明がつく。

つまり、平均約25133.5km／27.554550日に動的共通重心があるということになります。

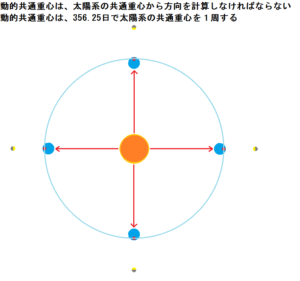
さて、重心のベクトルを計算して見ましょう。

図の様に、地球と月の動的共通重心は太陽系を356.25日で１周していると思うので、太陽系の動的共通重心からベクトルを測らなければならない。

私は習っていることに間違いがあると思っていますが、勉強をしている方は、テストでこの答えを書くと間違えますよ。(^^;

---

質量中心と重心の違いについて少し内容が難しいと思うので、私なりに考えて説明してみました。

勘違いしていなければいいのですが・・・。

参考程度にお読みください

以上